If you think about mountain ranges like the Andes or the Himalayas, you can come up with multiple factors that must affect their size and shape. Theres the collision of tectonic plates that squeezes them up into the air, of course. At a subduction zone where oceanic crust sinks downward beneath the continent, you can also sprout volcanos that grow skyward. On the other side of the ledger, various weathering and erosional processes sculpt the peaks. Streams cut sharp V-shaped valleys, while glaciers scrape out broad U-shaped ones instead. Either way, the end result is that the high places are gradually worn down, their rock scattered into the lowlands.
So what, exactly, is the primary control on the ranges height? Is it just a function of the plate tectonic forces? Or does climate dictate things by setting the rate at which the peaks are consumed?
This is an actual topic of considerable debate in geology, with arguments going both ways. A team led by Armin Dielforder at the GFZ German Research Centre for Geosciences wanted to test these hypotheses in a new way. The researchers set out to calculate the theoretical height of mountain ranges based purely on the tectonic forces. If erosion is dominant, you would see big mismatches between theoretical and actual heights—hopefully varying along with factors that influence erosion, like the climate.
Calculating the theoretical height is a little harder than it sounds, though. GPS measurements of plate motion arent enough to figure out the forces involved, just as the speed of two cars isnt really enough to predict the outcome of a collision. So the researchers used published estimates of a number of factors for 10 plate-collision mountain ranges. Based on earthquake data, seismic imaging of fault zones, and other measurements, researchers can work out: 1) the angle of the fault, 2) the strength of the fault, and 3) the depth at which rocks along the fault begin to deform in a ductile way, more like putty. Put all that together and you can get the shear force along that fault.
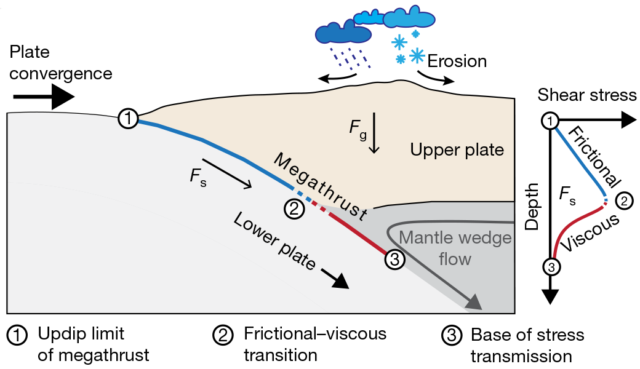
Feeding this into a mathematical model, the researchers calculated how tall a mountain range could be sustained with that shear force. The more mass that gets squeezed up into the air, of course, the stronger the gravitational force that would push it back down and spread it out. Those are the forces balancing against each other here. And while were focused on the mountains, you also have to account for the seafloor topography being supported, as the continental plates where the mountains are bulge upward from the trench where the two plates meet.
With predictions in hand, the team compared them to the average heights for each stretch of mountains, measured from the trench. Along the northern half of Japan, for example, the method predicts a height of about 0.8 kilometers, while the Himalayas come in at about 6 kilometers. Both those numbers are pretty good, and all the predicted heights matched the real heights within the error bars. That means the forces from plate tectonics seem to account for the height of the mountains, without any additional influences.

arstechnica
[contfnewc] [contfnewc]






